Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus. Given afunction f of a real variable x and an interval [a, b] of the real line, the definite integral
is defined informally to be the signed area of the region in the xy-plane bounded by the graph of f, the x-axis, and the vertical lines x = a and x = b, such that area above the x-axis adds to the total, and that below the x-axis subtracts from the total.
The term integral may also refer to the notion of the antiderivative, a function F whose derivative is the given function f. In this case, it is called anindefinite integral and is written:
The integrals discussed in this article are termed definite integrals.
The principles of integration were formulated independently by Isaac Newton and Gottfried Leibniz in the late 17th century. Through the fundamental theorem of calculus, which they independently developed, integration is connected with differentiation: if f is a continuous real-valued function defined on a closed interval [a, b], then, once an antiderivative F of f is known, the definite integral of f over that interval is given by
Integrals and derivatives became the basic tools of calculus, with numerous applications in science and engineering. The founders of the calculus thought of the integral as an infinite sum of rectangles of infinitesimal width. A rigorous mathematical definition of the integral was given by Bernhard Riemann. It is based on a limiting procedure which approximates the area of a curvilinear region by breaking the region into thin vertical slabs. Beginning in the nineteenth century, more sophisticated notions of integrals began to appear, where the type of the function as well as the domain over which the integration is performed has been generalised. A line integral is defined for functions of two or three variables, and the interval of integration [a, b] is replaced by a certain curve connecting two points on the plane or in the space. In a surface integral, the curve is replaced by a piece of a surface in the three-dimensional space. Integrals of differential forms play a fundamental role in modern differential geometry. These generalizations of integrals first arose from the needs of physics, and they play an important role in the formulation of many physical laws, notably those of electrodynamics. There are many modern concepts of integration, among these, the most common is based on the abstract mathematical theory known as Lebesgue integration, developed by Henri Lebesgue.
Calculus
Fundamental theorem
Limits of functions
Continuity
Mean value theorem
Rolle's theorem
Differential calculus
Integral calculus
Lists of integrals
Definitions
Antiderivative Integral Improper integral Riemann integral Lebesgue integration Contour integral
Integration by
parts discs cylindrical shells substitution trigonometric substitution partial fractions changing order reduction formulae
Series
Vector calculus
Multivariable calculus
Specialized calculi
INTEGERS
Fundamental theorem
Limits of functions
Continuity
Mean value theorem
Rolle's theorem
Differential calculus
Integral calculus
Lists of integrals
Definitions
Antiderivative Integral Improper integral Riemann integral Lebesgue integration Contour integral
Integration by
parts discs cylindrical shells substitution trigonometric substitution partial fractions changing order reduction formulae
Series
Vector calculus
Multivariable calculus
Specialized calculi
INTEGERS
An integer is a number that can be written without a fractional or decimal component. For example, 21, 4, and −2048 are integers; 9.75, 5½, and √2 are not integers. The set of integers is a subset of the real numbers, and consists of the natural numbers (0, 1, 2, 3, ...) and the negatives of the non-zero natural numbers (−1, −2, −3, ...).
The name derives from the Latin integer (meaning literally "untouched," hence "whole": the word entire comes from the same origin, but via French[1]). The set of all integers is often denoted by a boldface Z (or blackboard bold  , Unicode U+2124 ℤ), which stands for Zahlen (German for numbers, pronounced [ˈtsaːlən]).[2]
, Unicode U+2124 ℤ), which stands for Zahlen (German for numbers, pronounced [ˈtsaːlən]).[2]
The integers (with addition as operation) form the smallest group containing the additive monoid of the natural numbers. Like the natural numbers, the integers form acountably infinite set. In algebraic number theory, these commonly understood integers, embedded in the field of rational numbers, are referred to as rational integers to distinguish them from the more broadly defined algebraic integers.
http://en.wikipedia.org/wiki/Integer
http://en.wikipedia.org/wiki/Integer
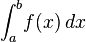

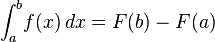

No comments:
Post a Comment